Calculates permutation importance for a set of features or a set of feature groups.
By default, importance is calculated for all columns in X (except column names
used as response y or as case weight w).
perm_importance(object, ...)
# Default S3 method
perm_importance(
object,
X,
y,
v = NULL,
pred_fun = stats::predict,
loss = "squared_error",
m_rep = 4L,
agg_cols = FALSE,
normalize = FALSE,
n_max = 10000L,
w = NULL,
verbose = TRUE,
...
)
# S3 method for class 'ranger'
perm_importance(
object,
X,
y,
v = NULL,
pred_fun = function(m, X, ...) stats::predict(m, X, ...)$predictions,
loss = "squared_error",
m_rep = 4L,
agg_cols = FALSE,
normalize = FALSE,
n_max = 10000L,
w = NULL,
verbose = TRUE,
...
)
# S3 method for class 'explainer'
perm_importance(
object,
X = object[["data"]],
y = object[["y"]],
v = NULL,
pred_fun = object[["predict_function"]],
loss = "squared_error",
m_rep = 4L,
agg_cols = FALSE,
normalize = FALSE,
n_max = 10000L,
w = object[["weights"]],
verbose = TRUE,
...
)Arguments
- object
Fitted model object.
- ...
Additional arguments passed to
pred_fun(object, X, ...), for instancetype = "response"in aglm()model, orreshape = TRUEin a multiclass XGBoost model.- X
A data.frame or matrix serving as background dataset.
- y
Vector/matrix of the response, or the corresponding column names in
X.- v
Vector of feature names, or named list of feature groups. The default (
NULL) will use all column names ofXwith the following exception: Ifyorware passed as column names, they are dropped.- pred_fun
Prediction function of the form
function(object, X, ...), providing \(K \ge 1\) predictions per row. Its first argument represents the modelobject, its second argument a data structure likeX. Additional arguments (such astype = "response"in a GLM, orreshape = TRUEin a multiclass XGBoost model) can be passed via.... The default,stats::predict(), will work in most cases.- loss
One of "squared_error", "logloss", "mlogloss", "poisson", "gamma", or "absolute_error". Alternatively, a loss function can be provided that turns observed and predicted values into a numeric vector or matrix of unit losses of the same length as
X. For "mlogloss", the responseycan either be a dummy matrix or a discrete vector. The latter case is handled via a fast version ofmodel.matrix(~ as.factor(y) + 0). For "squared_error", the response can be a factor with levels in column order of the predictions. In this case, squared error is evaluated for each one-hot-encoded column.- m_rep
Number of permutations (default 4).
- agg_cols
Should multivariate losses be summed up? Default is
FALSE. In combination with the squared error loss,agg_cols = TRUEgives the Brier score for (probabilistic) classification.- normalize
Should importance statistics be divided by average loss? Default is
FALSE. IfTRUE, an importance of 1 means that the average loss has been doubled by shuffling that feature's column.- n_max
If
Xhas more thann_maxrows, a random sample ofn_maxrows is selected fromX. In this case, set a random seed for reproducibility.- w
Optional vector of case weights. Can also be a column name of
X.- verbose
Should a progress bar be shown? The default is
TRUE.
Value
An object of class "hstats_matrix" containing these elements:
M: Matrix of statistics (one column per prediction dimension), orNULL.SE: Matrix with standard errors ofM, orNULL. Multiply withsqrt(m_rep)to get standard deviations instead. Currently, supported only forperm_importance().m_rep: The number of repetitions behind standard errorsSE, orNULL. Currently, supported only forperm_importance().statistic: Name of the function that generated the statistic.description: Description of the statistic.
Details
The permutation importance of a feature is defined as the increase in the average
loss when shuffling the corresponding feature values before calculating predictions.
By default, the process is repeated m_rep = 4 times, and the results are averaged.
In most of the cases, importance values should be derived from an independent test
data set. Set normalize = TRUE to get relative increases in average loss.
Methods (by class)
perm_importance(default): Default method.perm_importance(ranger): Method for "ranger" models.perm_importance(explainer): Method for DALEX "explainer".
Losses
The default loss is the "squared_error". Other choices:
"absolute_error": The absolute error is the loss corresponding to median regression.
"poisson": Unit Poisson deviance, i.e., the loss function used in Poisson regression. Actual values
yand predictions must be non-negative."gamma": Unit gamma deviance, i.e., the loss function of Gamma regression. Actual values
yand predictions must be positive."logloss": The Log Loss is the loss function used in logistic regression, and the top choice in probabilistic binary classification. Responses
yand predictions must be between 0 and 1. Predictions represent probabilities of having a "1"."mlogloss": Multi-Log-Loss is the natural loss function in probabilistic multi-class situations. If there are K classes and n observations, the predictions form a (n x K) matrix of probabilities (with row-sums 1). The observed values
yare either passed as (n x K) dummy matrix, or as discrete vector with corresponding levels. The latter case is turned into a dummy matrix by a fast version ofmodel.matrix(~ as.factor(y) + 0).A function with signature
f(actual, predicted), returning a numeric vector or matrix of the same length as the input.
References
Fisher A., Rudin C., Dominici F. (2018). All Models are Wrong but many are Useful: Variable Importance for Black-Box, Proprietary, or Misspecified Prediction Models, using Model Class Reliance. Arxiv.
Examples
# MODEL 1: Linear regression
fit <- lm(Sepal.Length ~ ., data = iris)
s <- perm_importance(fit, X = iris, y = "Sepal.Length")
#>
|
| | 0%
|
|================== | 25%
|
|=================================== | 50%
|
|==================================================== | 75%
|
|======================================================================| 100%
s
#> Permutation importance
#> Petal.Length Species Petal.Width Sepal.Width
#> 3.89841599 0.35511950 0.11329728 0.09801916
s$M
#> [,1]
#> Petal.Length 3.89841599
#> Species 0.35511950
#> Petal.Width 0.11329728
#> Sepal.Width 0.09801916
s$SE # Standard errors are available thanks to repeated shuffling
#> [,1]
#> Petal.Length 0.226550540
#> Species 0.023463859
#> Petal.Width 0.003875789
#> Sepal.Width 0.010737274
plot(s)
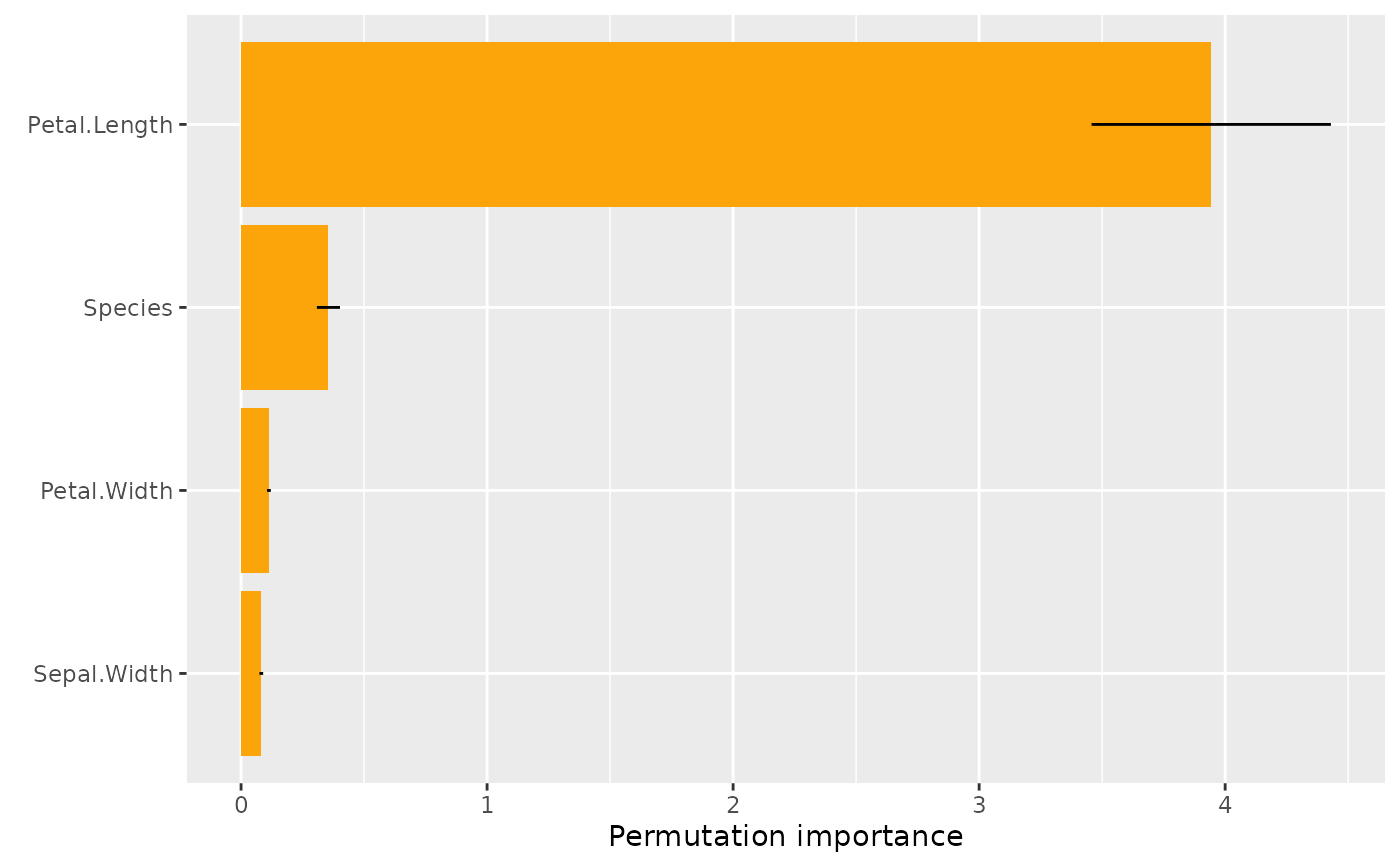
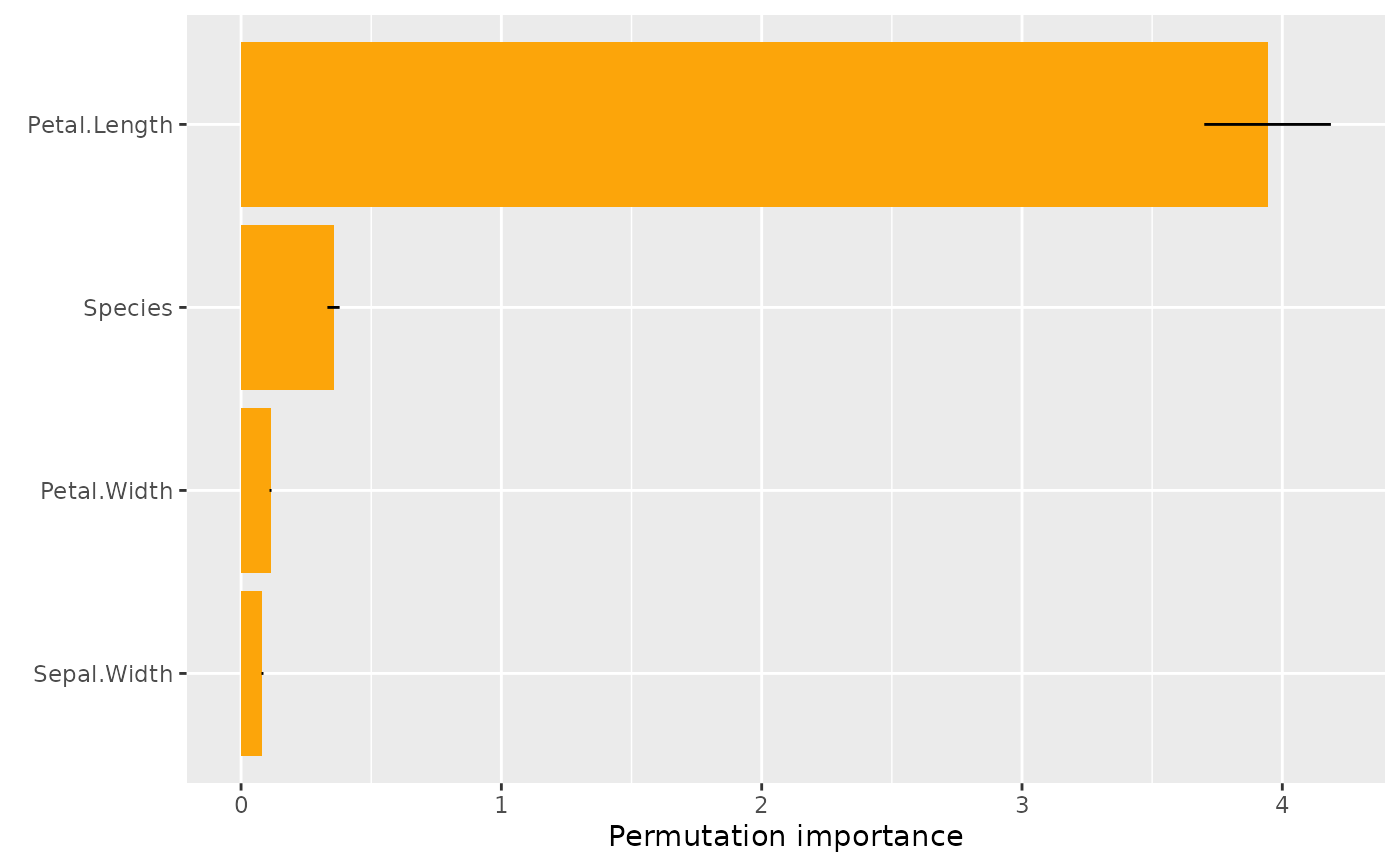 plot(s, err_type = "SD") # Standard deviations instead of standard errors
plot(s, err_type = "SD") # Standard deviations instead of standard errors
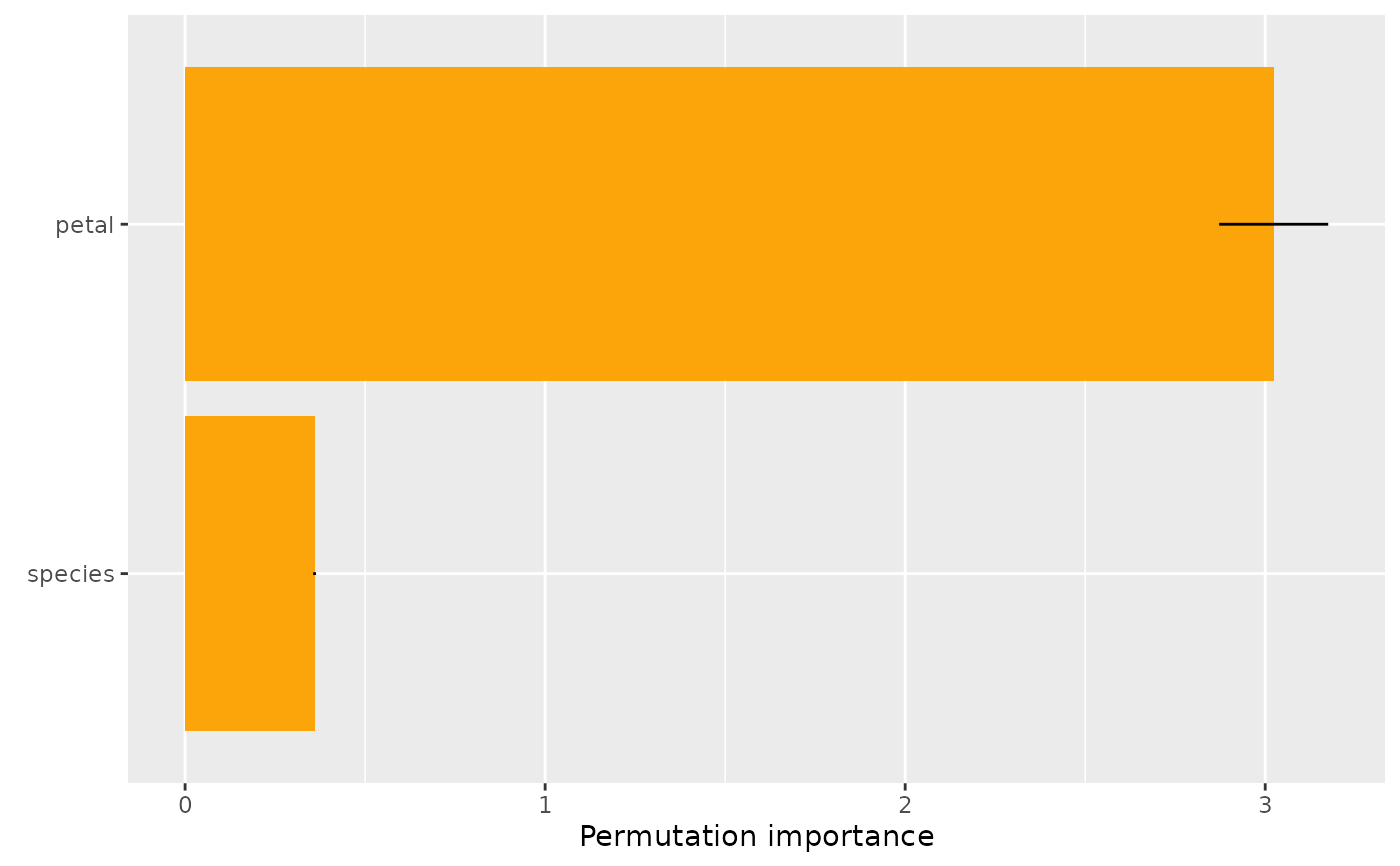
 # Groups of features can be passed as named list
v <- list(petal = c("Petal.Length", "Petal.Width"), species = "Species")
s <- perm_importance(fit, X = iris, y = "Sepal.Length", v = v, verbose = FALSE)
s
#> Permutation importance
#> petal species
#> 3.0235937 0.3596812
plot(s)
# Groups of features can be passed as named list
v <- list(petal = c("Petal.Length", "Petal.Width"), species = "Species")
s <- perm_importance(fit, X = iris, y = "Sepal.Length", v = v, verbose = FALSE)
s
#> Permutation importance
#> petal species
#> 3.0235937 0.3596812
plot(s)
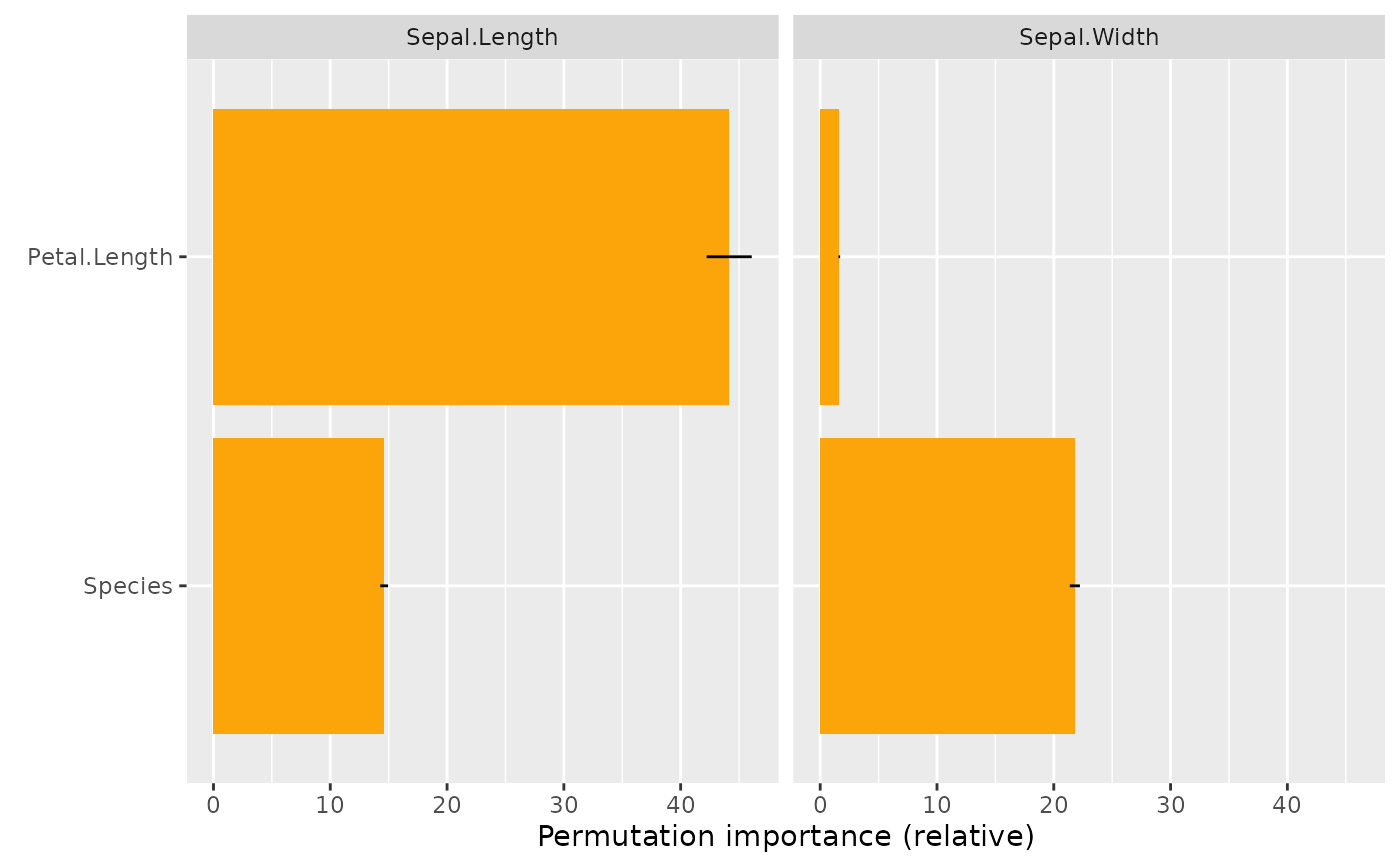
 # MODEL 2: Multi-response linear regression
fit <- lm(as.matrix(iris[, 1:2]) ~ Petal.Length + Petal.Width + Species, data = iris)
s <- perm_importance(fit, X = iris[, 3:5], y = iris[, 1:2], normalize = TRUE)
#>
|
| | 0%
|
|======================= | 33%
|
|=============================================== | 67%
|
|======================================================================| 100%
s
#> Permutation importance (relative)
#> Sepal.Length Sepal.Width
#> Petal.Length 44.1555884272 1.638492
#> Species 14.6144263498 21.806533
#> Petal.Width -0.0002101401 5.176280
plot(s)
# MODEL 2: Multi-response linear regression
fit <- lm(as.matrix(iris[, 1:2]) ~ Petal.Length + Petal.Width + Species, data = iris)
s <- perm_importance(fit, X = iris[, 3:5], y = iris[, 1:2], normalize = TRUE)
#>
|
| | 0%
|
|======================= | 33%
|
|=============================================== | 67%
|
|======================================================================| 100%
s
#> Permutation importance (relative)
#> Sepal.Length Sepal.Width
#> Petal.Length 44.1555884272 1.638492
#> Species 14.6144263498 21.806533
#> Petal.Width -0.0002101401 5.176280
plot(s)
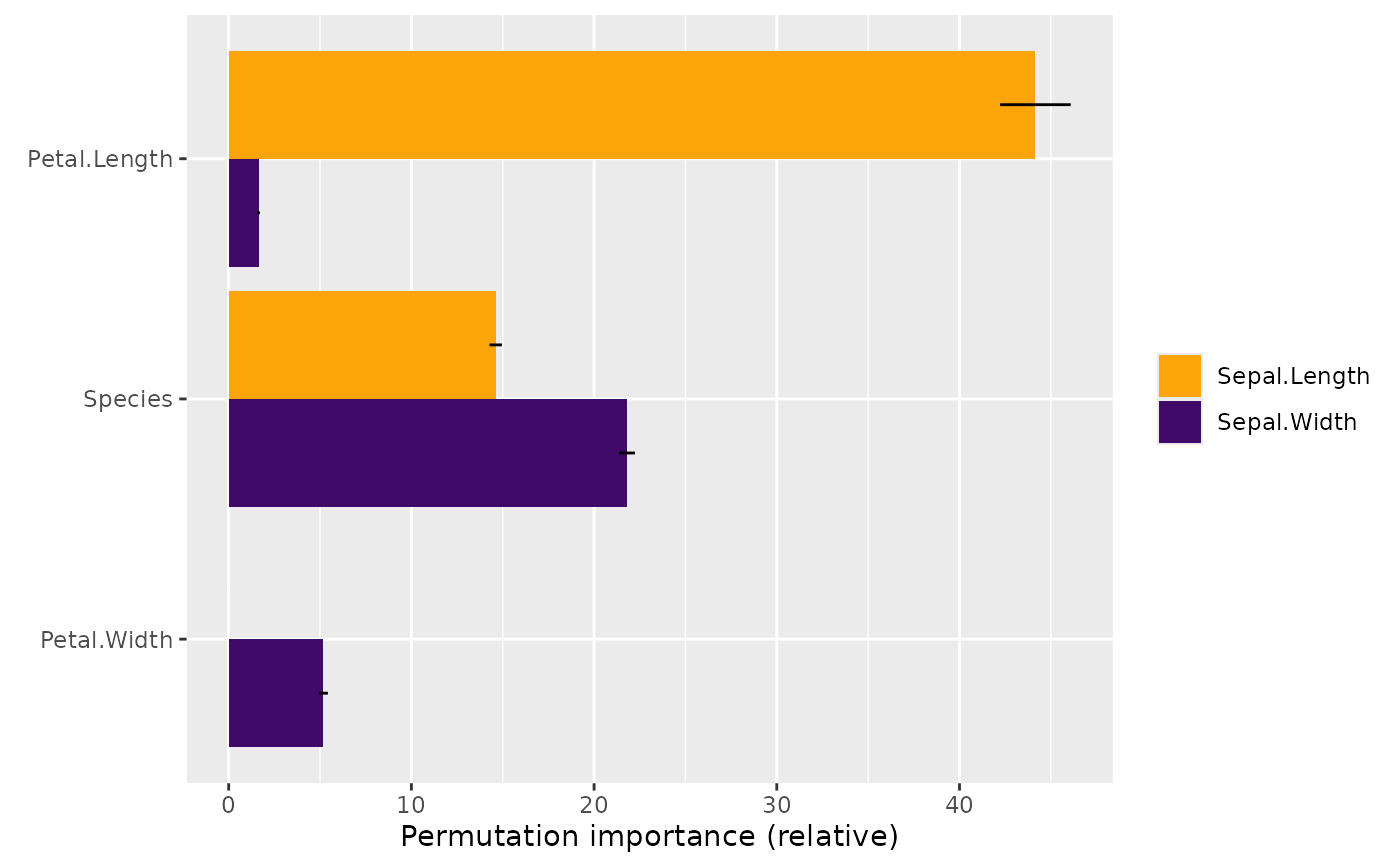 plot(s, swap_dim = TRUE, top_m = 2)
plot(s, swap_dim = TRUE, top_m = 2)